15 Prueba de hipótesis para la comparación de dos medias
- Autor: Edsaúl Emilio Pérez Guerrero
- Afiliación: Universidad de Guadalajara
- mail: edsaul.perezg@academicos.udg.mx
- Última actualización: 2024-04-24
En este capítulo se revisará la comparación de variables de tipo cuantitivo entre dos o más grupos, a saber, las pruebas de hipótesis que se revisarán son:
- Prueba t para variables independientes
- Prueba t para variables dependientes
15.1 Prueba t y distritución t
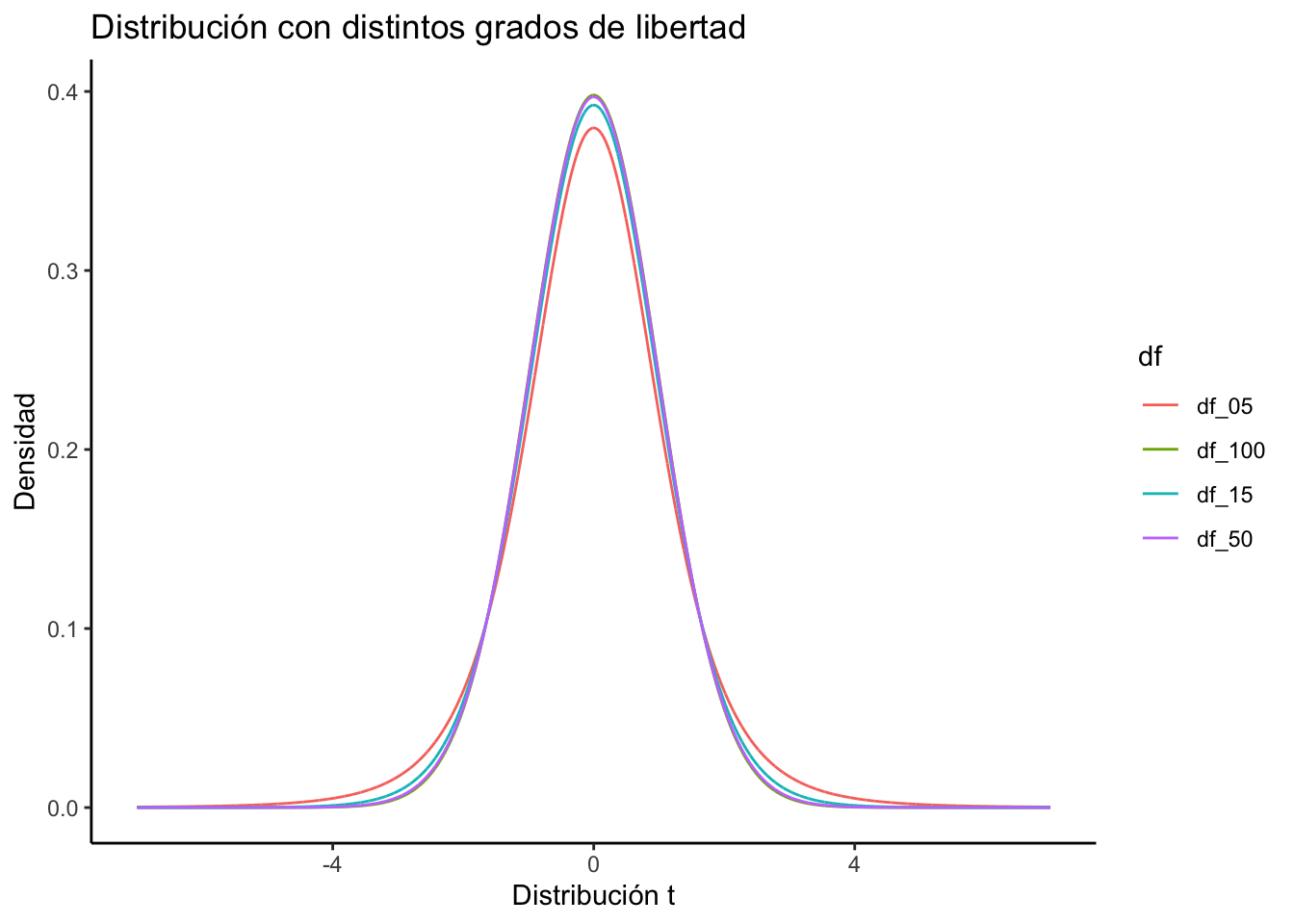
La prueba t de student se basa en la distribución t, que presenta las siguientes características:
- Tiene media de 0.
- Es simétrica con respecto a la media.
- Varianza mayor que 1. Aunque tiene a 1 cuando la \(n\) aumenta.
- La variable \(t\) va de.
- Es una familia de distribuciones. Hay una distribución para cada valor de \(n\).
- Es menos espigada y mas alargada que la distribución normal.
- Se aproxima a la distribución normal a medida que \(n-1\) se aproxima al infinito.
En la figura Figure 15.1 se muestran distintas distribuciones t de acuerdo con sus grados de libertad.
Dentro de las pruebas t, existen diferente variantes, cada una de ella para situaciones en particular. Por ejemplo, existe una prueba t para grupos pareados, otra para grupos independientes etc. La ?fig-13-2 muestra un resumen de las diferentes pruebas t. No olvide: Muchas maneras estimar t, pero la misma moneda de cambio^
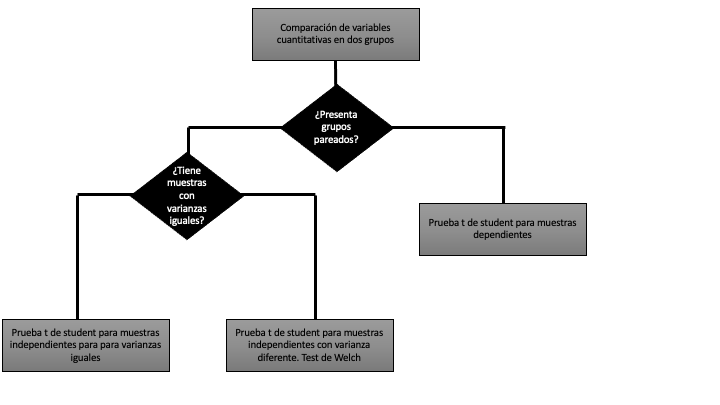{#fig-13-2 width=100% fig-align=“center” f}
15.2 Comparación de dos medias con varianzas iguales y grupos independientes
La prueba t de student para muestras independientes se utiliza para la comparación de medias de grupos independientes. En general las hipótesis que se pueden plantear son:
| \(H_O\) | \(H_A\) | Tipo de hipótesis | |
|---|---|---|---|
| 1 | \(\mu_1- \mu_2 =0\) | \(\mu_1- \mu_2 \neq0\) | Bilateral |
| 2 | \(\mu_1- \mu_2 >=0\) | \(\mu_1- \mu_2 \ <0\) | Unilateral |
| 3 | \(\mu_1- \mu_2 <=0\) | \(\mu_1- \mu_2 \ >0\) | Unilateral |
En R podemos utilizar la función t.test() que posee los siguientes argumentos:
X: un vector numérico (no vacío) de valores de datos.
y: un vector numérico opcional (no vacío) de valores de datos.
alternative: una cadena de caracteres que especifica el tipo de hipótesis. Las opciones a saber son: “two.sided” (default) para una hipótesis bilateral, “greater” cuando se quiere probar si la media 1 es mayor que la media 2 o “less” (lo contrario a greater). Puede especificar solo la letra inicial.
paired: una indicación lógica si desea una prueba t pareada.
var.equal: una variable lógica que indica si se deben tratar las dos varianzas como si fueran iguales. Si es VERDADERO, la varianza agrupada se usa para estimar la varianza; de lo contrario, se usa la aproximación de Welch (o Satterthwaite) a los grados de libertad.
conf.level: nivel de confianza del intervalo.
formula: se utiliza para introducir los datos a manera de formula.
data: Argumento que se utilza para identificar el data frame del que provienen los datos. Si se usó la función
attach()o el simbolo de$no es necesario utilizar este argumento.
En R la función t.test se puede utilizar de dos formas:
- Utilizando “x” y “y”: t.test(x=objeto1, y=objeto2)
- Utilizando la formula: t.test(Variable de prueba~Variable agrupación)
La primera opción se utiliza cuando las variables a comparar se encuentran en columnas separadas, mientras que la segunda, se utiliza cuando mi variable cuantitativa se encuentra en un columna para ambos grupos, y mi variable de agrupación (factor) en otra columna.
Vamos a resolver un ejemplo
15.2.1 Ejercicio de practica para la prueba t para muestras independientes (emx-86?)
Example 15.1 Un estudio de los investigadores Eidelman et al.tiene como objetivo examinar las características de destrucción pulmonar en personas que fuman cigarros antes de desarrollar un marcado enfisema pulmonar. Se practicaron mediciones de tres indices de destrucción pulmonar en los pulmones de personas longevas que no fumaban y en personas con tabaquismo que murieron repentinamente fuera del hospital por causas no respiratorias. Una calificación alta indica un mayor daño pulmonar. Los datos fueron guardados en dos objetos para uno de los índices de destrucción pulmonar de una muestra de 9 personas que no fuman y 16 fumadores. Se pretende saber si es posible concluir, con base en los datos, que las personas que sí fuman, en general, tienen los pulmones mas dañados que las personas no fumadoras, como lo indican las mediciones. No se conocen las variancias poblacionales, pero se supone que son iguales. Utilice un nivel de confianza del 98%. (ejercio obtenido del libro de Bioestadística de Daniels)
Para la resolución de este ejercicio vamos a crear dos objetos, uno para la calificación de los fumadores y otro para la calificación de los no fumadores:
Calif_No_Fumadores<-c(18.1,6.0,10.8,11.0,7.7,17.9,8.5,13.0,18.9)
Calif_Fumadores<- c(16.6,13.9,11.3,26.5, 17.4, 15.3, 15.8, 12.3,
18.6, 12.0, 24.1, 16.5, 21.8, 16.3, 23.4,
18.8)Lo primero es graficar, podemos hacerlo mediante un boxplot. Más adelante utilizaremos la función plotmeans()
boxplot(Calif_Fumadores, Calif_No_Fumadores, ylab="Calificaciones",
main="Calificación de daño pulmonar", col=c("cadetblue", "cadetblue2"),
names = c("Fumadores", "No fumadores"), frame = FALSE)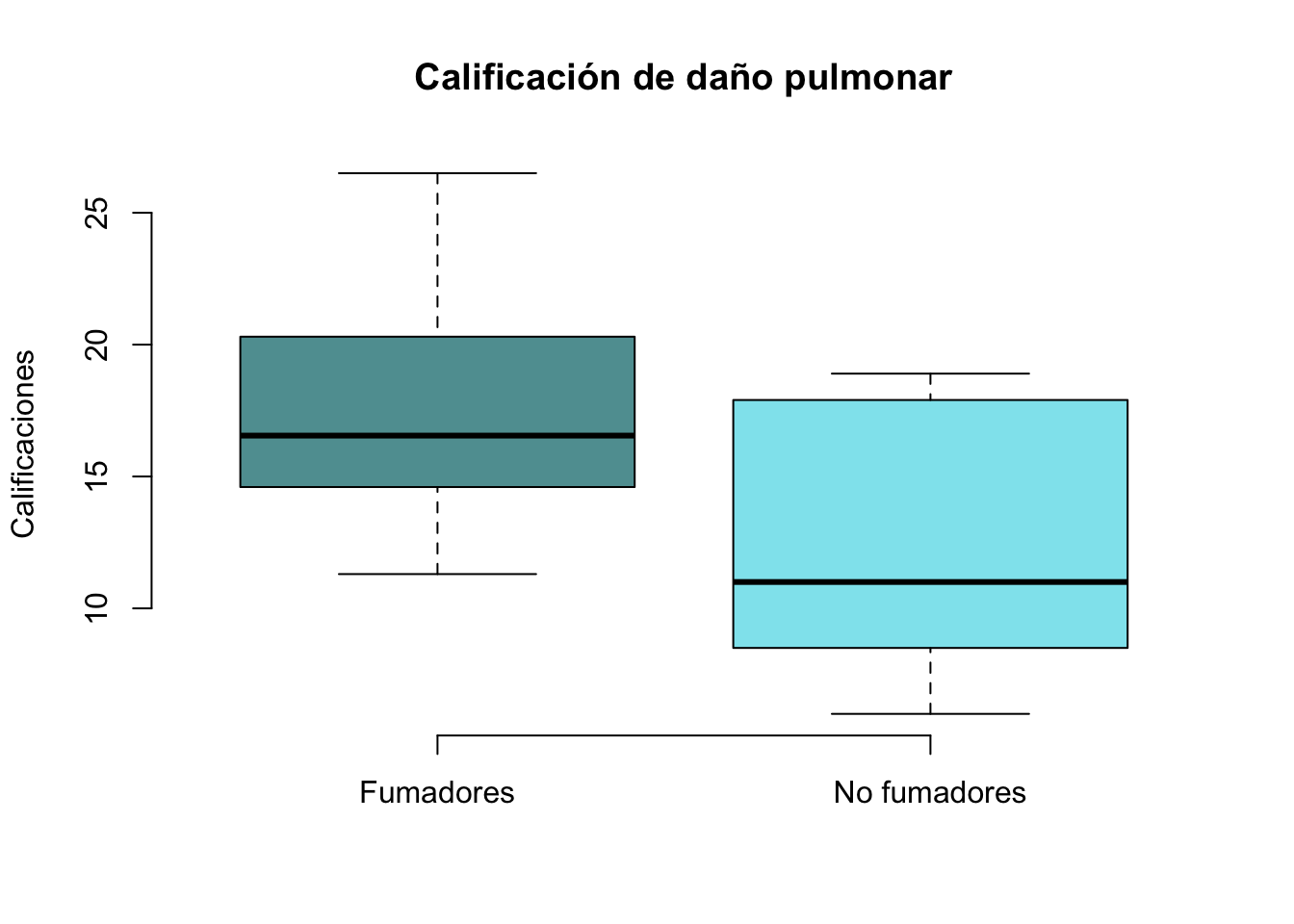 
La gráfica anterior parece indicar que la calificación en el grupo de fumadores es mayor que en el grupo de los no fumadores. Vamos a comprobarlo mediante la prueba t de student.
t.test(Calif_Fumadores, Calif_No_Fumadores, alternative = "greater",
conf.level = 0.98, var.equal = T)
Two Sample t-test
data: Calif_Fumadores and Calif_No_Fumadores
t = 2.658, df = 23, p-value = 0.007027
alternative hypothesis: true difference in means is greater than 0
98 percent confidence interval:
0.9237087 Inf
sample estimates:
mean of x mean of y
17.53750 12.43333 Utilizamos el argumento alternative="greater" ya que nos interesa probar que la calificación de los fumadores es mayor que los no fumadores (la media del grupo es mayor que la media del grupo 2). Además, utilizamos un nivel de confianza del 98%. De momento asumimos que ambos grupos tienen varianzas iguales.
Supongamos ahora que es nuestro interés conocer que simplemente si las medias son diferentes y cambiamos el argumento alternative="two.sided".
t.test(Calif_Fumadores, Calif_No_Fumadores, alternative = "two.sided",
conf.level = 0.98, var.equal = T)
Two Sample t-test
data: Calif_Fumadores and Calif_No_Fumadores
t = 2.658, df = 23, p-value = 0.01405
alternative hypothesis: true difference in means is not equal to 0
98 percent confidence interval:
0.3036205 9.9047128
sample estimates:
mean of x mean of y
17.53750 12.43333 Aunque podría omitir el argumento alternative="two.sided" ya que por se encuentra predefinido. El siguiente código dará el mismo resultado:
t.test(Calif_Fumadores, Calif_No_Fumadores,
conf.level = 0.98, var.equal = T)
Two Sample t-test
data: Calif_Fumadores and Calif_No_Fumadores
t = 2.658, df = 23, p-value = 0.01405
alternative hypothesis: true difference in means is not equal to 0
98 percent confidence interval:
0.3036205 9.9047128
sample estimates:
mean of x mean of y
17.53750 12.43333 Otra opción para utilizar la función t.test() es mediante el uso de formula. Para ello, vamos a importar la base de datos Calif_Fum utilizando el menú de RStudio. Asegúrese de que su objeto fue nombrado como Calif_Fum.
Ahora ya podemos utilizar la función t.test() como formula:
t.test(Calif_Fum$Calificacion~Calif_Fum$Grupo, conf.level = 0.98, var.equal = T)
Two Sample t-test
data: Calif_Fum$Calificacion by Calif_Fum$Grupo
t = 2.658, df = 23, p-value = 0.01405
alternative hypothesis: true difference in means between group Fumadores and group No Fumadores is not equal to 0
98 percent confidence interval:
0.3036205 9.9047128
sample estimates:
mean in group Fumadores mean in group No Fumadores
17.53750 12.43333 También ahora ya podemos hacer un gráficos de medias, si es necesario instale la librería gplots
library(gplots)
Attaching package: 'gplots'The following object is masked from 'package:stats':
lowessplotmeans(Calif_Fum$Calificacion~Calif_Fum$Grupo, xlab="Grupos de estudio", ylab="Calificación")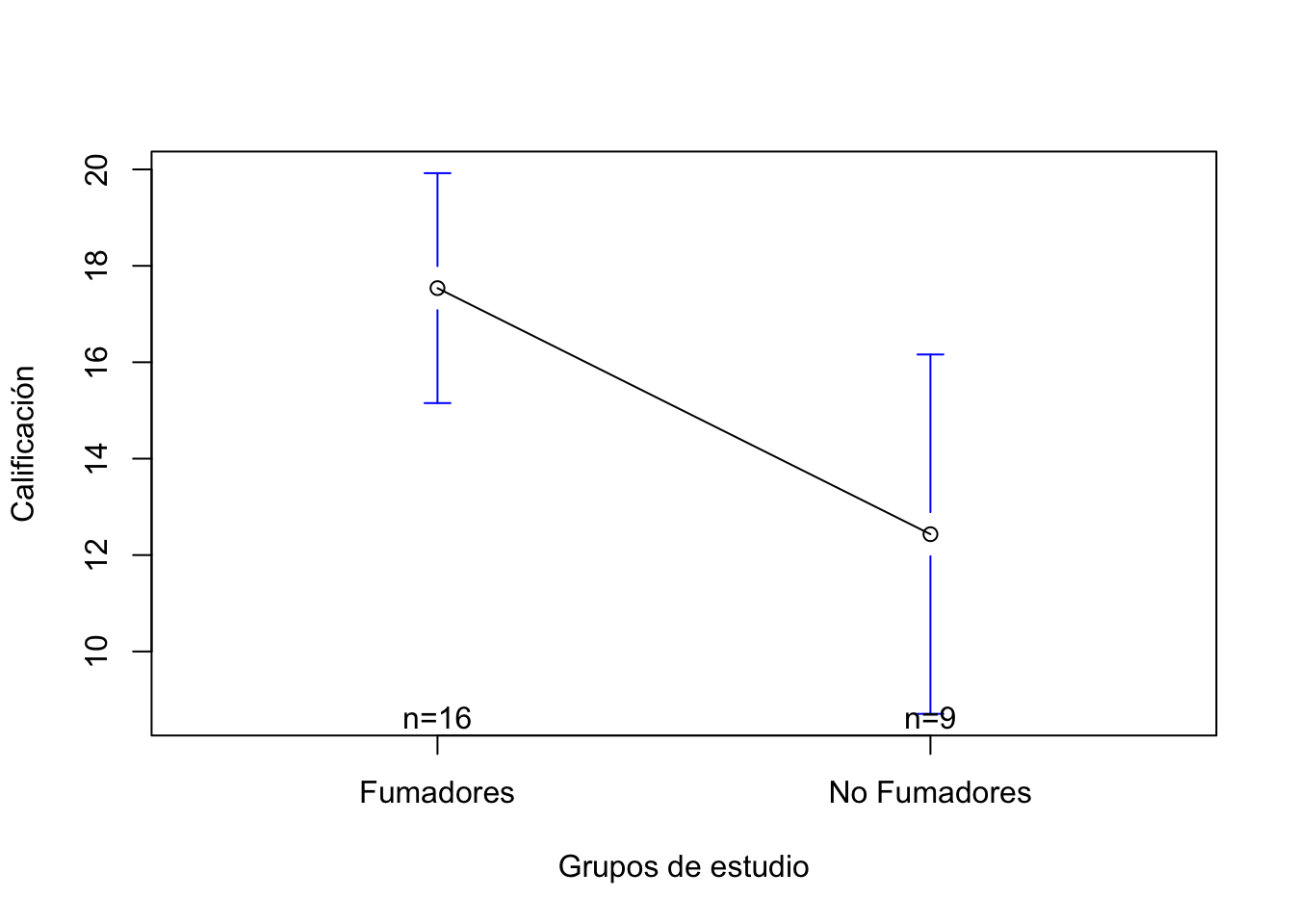
15.3 Comparación de dos medias con varianzas diferentes y grupos independientes
15.3.1 Test de welch
En estadística, la prueba t de Welch, o prueba t de varianzas desiguales, es una prueba de ubicación de dos muestras que se utiliza para probar la hipótesis de que dos poblaciones tienen medias iguales. Lleva el nombre de su creador, Bernard Lewis Welch, y es una adaptación de la prueba t de Student, y es más confiable cuando las dos muestras tienen varianzas desiguales y/o tamaños de muestra desiguales.
Para evaluar la igualdad de varianzas existen varias opciones, sin embargo, en este curso utilizaremos el test de barttlet mediante la función bartlett.test(). Utilizamos la base Calif_Fum.
bartlett.test(Calif_Fum$Calificacion~Calif_Fum$Grupo)
Bartlett test of homogeneity of variances
data: Calif_Fum$Calificacion by Calif_Fum$Grupo
Bartlett's K-squared = 0.065041, df = 1, p-value = 0.7987Note como es necesario introducir los datos como formula. La prueba nos dice que las varianzas son iguales entre los grupos.
A pesar del resultado, asumamos que las varianzas no son iguales para ejemplificar como realizar el test de welch cambiando el argumento var.equal = F
t.test(Calif_Fum$Calificacion~Calif_Fum$Grupo, conf.level = 0.98, var.equal = F)
Welch Two Sample t-test
data: Calif_Fum$Calificacion by Calif_Fum$Grupo
t = 2.5964, df = 15.593, p-value = 0.01978
alternative hypothesis: true difference in means between group Fumadores and group No Fumadores is not equal to 0
98 percent confidence interval:
0.01088222 10.19745111
sample estimates:
mean in group Fumadores mean in group No Fumadores
17.53750 12.43333 Otra manera de evaluar la homogenidad de varianzas es utilizar la prueba de levene con la función leveneTest de la librería car
car::leveneTest(Calif_Fum$Calificacion~Calif_Fum$Grupo)Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 1 0.1704 0.6836
23 15.4 Ejercicios para la prueba t de student para muestras independientes:
Solamente para los ejercicios del 15.1 al 15.3 debe de entregar/realizar lo siguiente:
- Preguntas ¿Qué quiero probar?¿Las medias son iguales? ¿las proporciones son distintas?¿Qué quiero hacer con mi prueba estadística?
- Hipótesis: Formular las hipótesis estadísticas
- Estadística descriptiva y Datos:
- Entender los datos
- Medidas descriptivas
- Gráficas
- Tomar en cuenta los datos con los que se cuenta:
- Medias
- variación
- Distribución
- Estadística de prueba: Tomando en cuenta mi hipótesis, la distribución de mis datos y los datos obtenidos del problema ¿Qué tipo de prueba voy a utilizar?
5.Evaluación de los supuestos + ¿Qué necesito cumplir para poder utilizar la prueba? + ¿Mis datos cumplen con los supuestos? + Si no se cumplen debo seleccionar otra prueba
- Regla de decisión:¿Que voy a considerar como mi valor crítico?¿Cual es mi zona de rechazo o aceptación?
- Estadístico de prueba: Determinar el valor de mi estadístico de prueba
- Decisión: ¿Acepto o rechazo?
- Conclusión
Los puntos anteriores fueron revisados en la presentación de clase sobre la prueba de hipótesis para la comparación de una media
Tome en cuenta que no en todos los ejercicios se podrán realizar todos los puntos.
Para el resto de los ejercicios (del 15.4 al 15.6) solamente entregue lo que se le solicita
Exercise 15.1 Evans et al. realizaron un estudio para determinar si la frecuencia y las características de los problemas geriátricos en pacientes de la tercera edad enfermos de diabetes presentan diferencias con respecto a pacientes de la misma edad pero sin diabetes. Los individuos estudiados, internados en una clínica, tenían de 70 a 90 años de edad. Entre los hallazgos de los investigadores están las siguientes estadísticas con respecto a las calificaciones en las medidores de los reflejos tendinosos profundos:
| Grupo | \(n\) | Media | \(sd\) |
|---|---|---|---|
| Sin diabetes | 79 | 2.1 | 1.1 |
| Con diabetes | 74 | 1.6 | 1.2 |
Se pretende saber si es posible concluir, con base en los datos, que, en promedio, los pacientes diabéticos tienen reflejos tendinosos profundos reducidos en comparación con pacientes sin diabetes de la misma edad. Utilice \(\alpha=0.01\).
Resuelva este problema asumiendo que: a) Las muestras tienen varianzas iguales b) Las muestras no tienen varianzas iguales (este inciso no es obligatorio, pero es preferible que lo resuelva)
Exercise 15.2 Un estudio de los investigadores Hommes et al. tiene dos propósitos: 1) investigar si el gasto de energía en reposo aumenta en la etapa primaria, sin síntomas de infección de VIH, y 2) estudiar las contribuciones relativas de la oxidación de carbohidratos de grasas durante el gasto de energía en reposo en los pacientes. Los individuos estudiados eran 11 pacientes externos varones infectados de VIH, que no presentaban síntomas y cuyas edades eran entre 23 y 50 años. El grupo de control estaba formado por 11 voluntarios varones sanos, con edades entre 25 y 51 anos, que resultaron físicamente normales en sus exámenes y expedientes médicos. Entre los hallazgos se tienen las estadísticas respecto a la medición del gasto de energía en reposo.
| Grupo | Media | \(sd\) |
|---|---|---|
| Individuos con VIH | 7116 | 173 |
| Individuos de control | 7058 | 205 |
¿Ofrecen estos datos suficiente evidencia que permita concluir que el gasto de energía en reposo aumenta durante la primera etapa, cuando no hay síntomas presentes de la infección de VIH? Utilice \(\alpha=05\). Asuma igualdad de varianzas.
Ejercicio tomado de BIOESTADÍSTICA, 4A ED Daniel , Wayne W.
Exercise 15.3 Frigerio et al. midieron la energía consumida en 32 mujeres de Gambia. Dieciséis de los individuos estudiados eran mujeres en periodo de lactancia (L) y el resto eran mujeres no embarazadas que no estaban en etapa de lactancia (NENL). Se reportaron los siguientes datos:
Para el grupo de mujeres en periodo de lactancia:
5289, 6209, 6054, 6665, 6343, 7699, 5678, 6954, 6916, 4770, 5979, 6305, 6502, 6113, 6347, 5657
Para el grupo de mujeres que no estaban en etapa de lactancia
9920, 8581, 9305, 10765, 8079, 9046, 7134, 8736, 10230, 7121, 8665, 5167, 8527, 7791, 8782, 6883
¿Proveen estos datos suficiente evidencia que permita concluir que las poblaciones muestreadas difieren respecto a la media de consumo de energía? Utilice \(\alpha=0.05\). Asuma igualdad de varianzas. Además obtenga un gráfico de caja y bigotes con los datos de cada grupo. Compruebe sus resultados utilizando la función de t.test.
Ejercicio adaptado de BIOESTADÍSTICA, 4A ED Daniel , Wayne W.
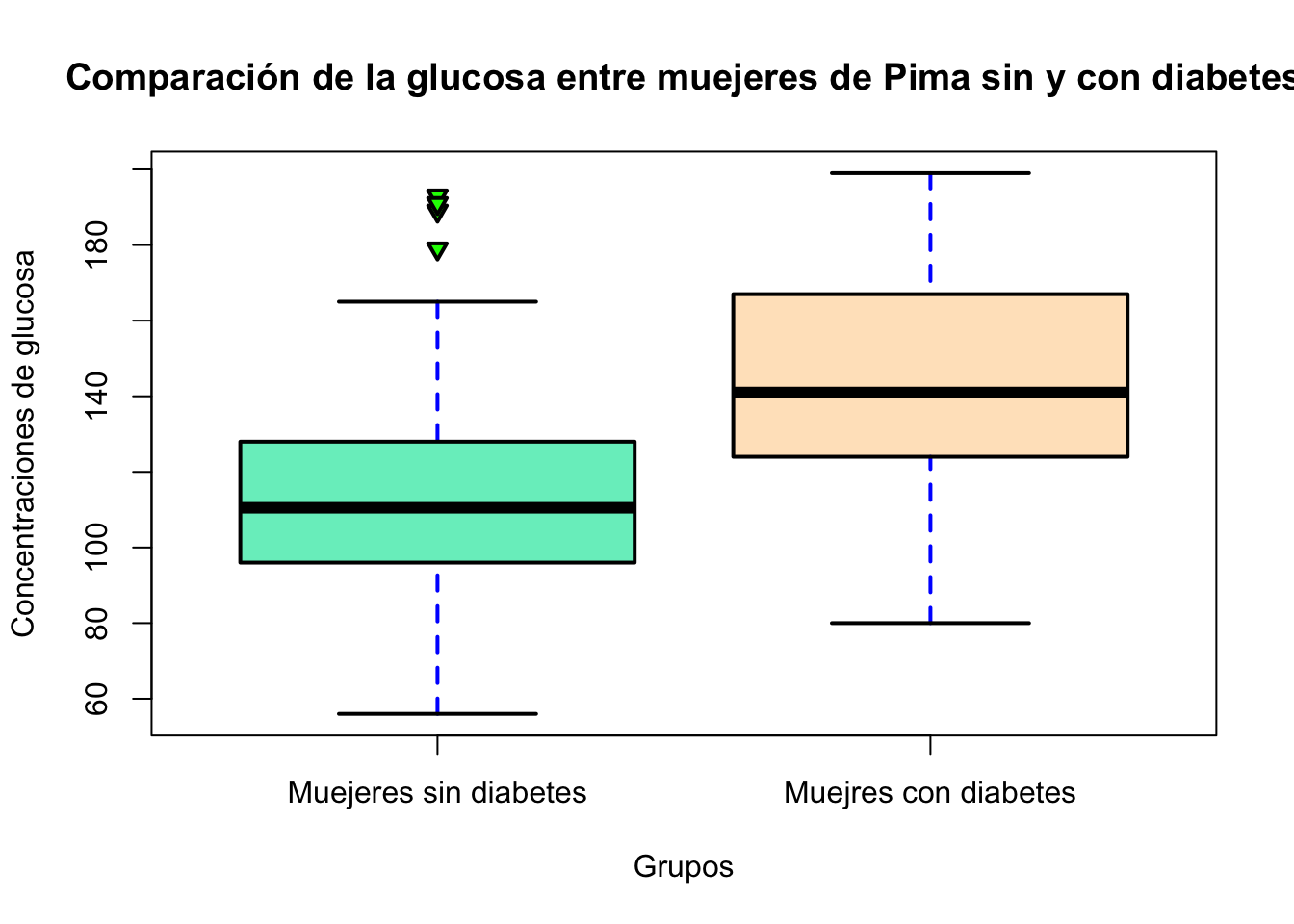
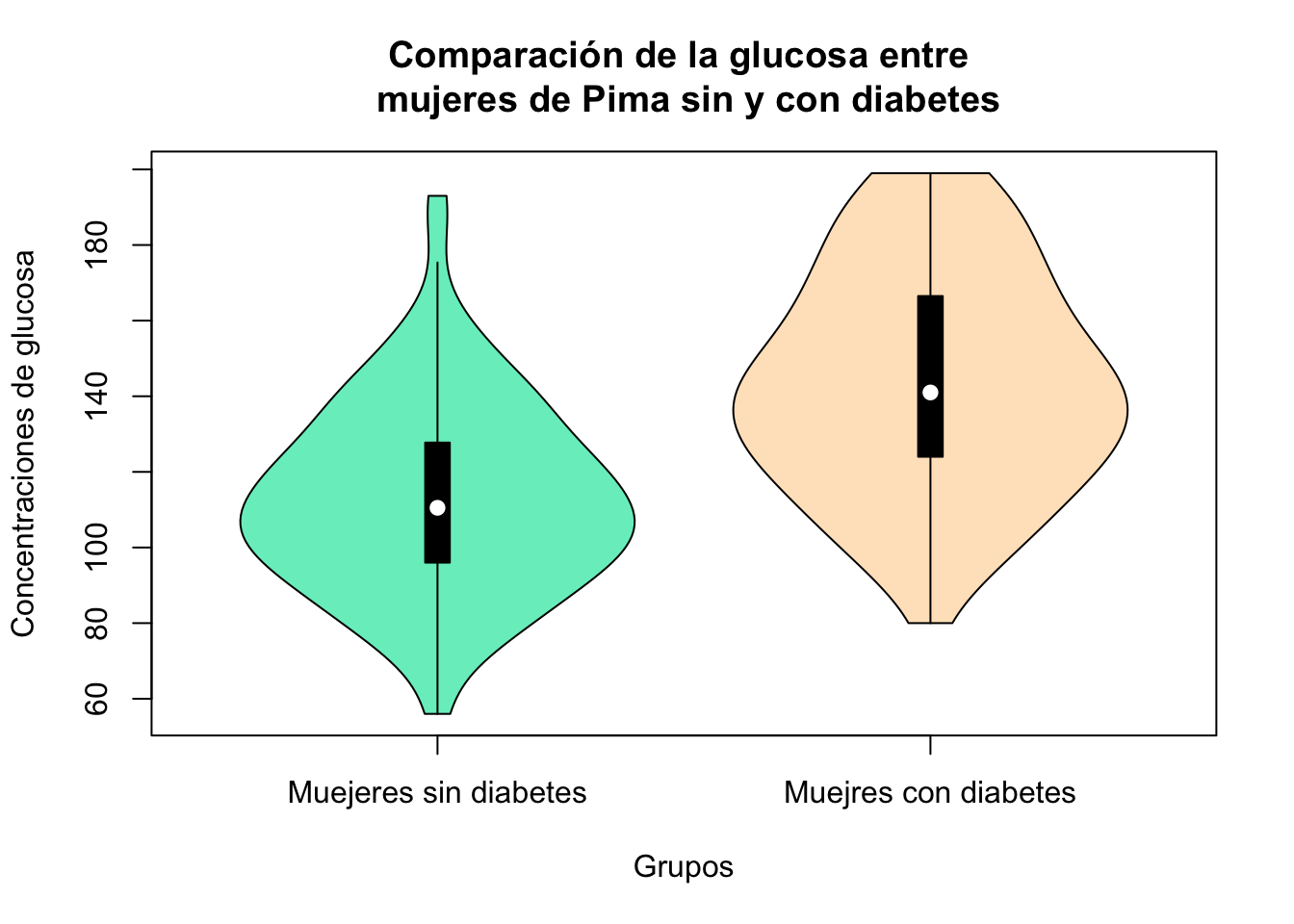
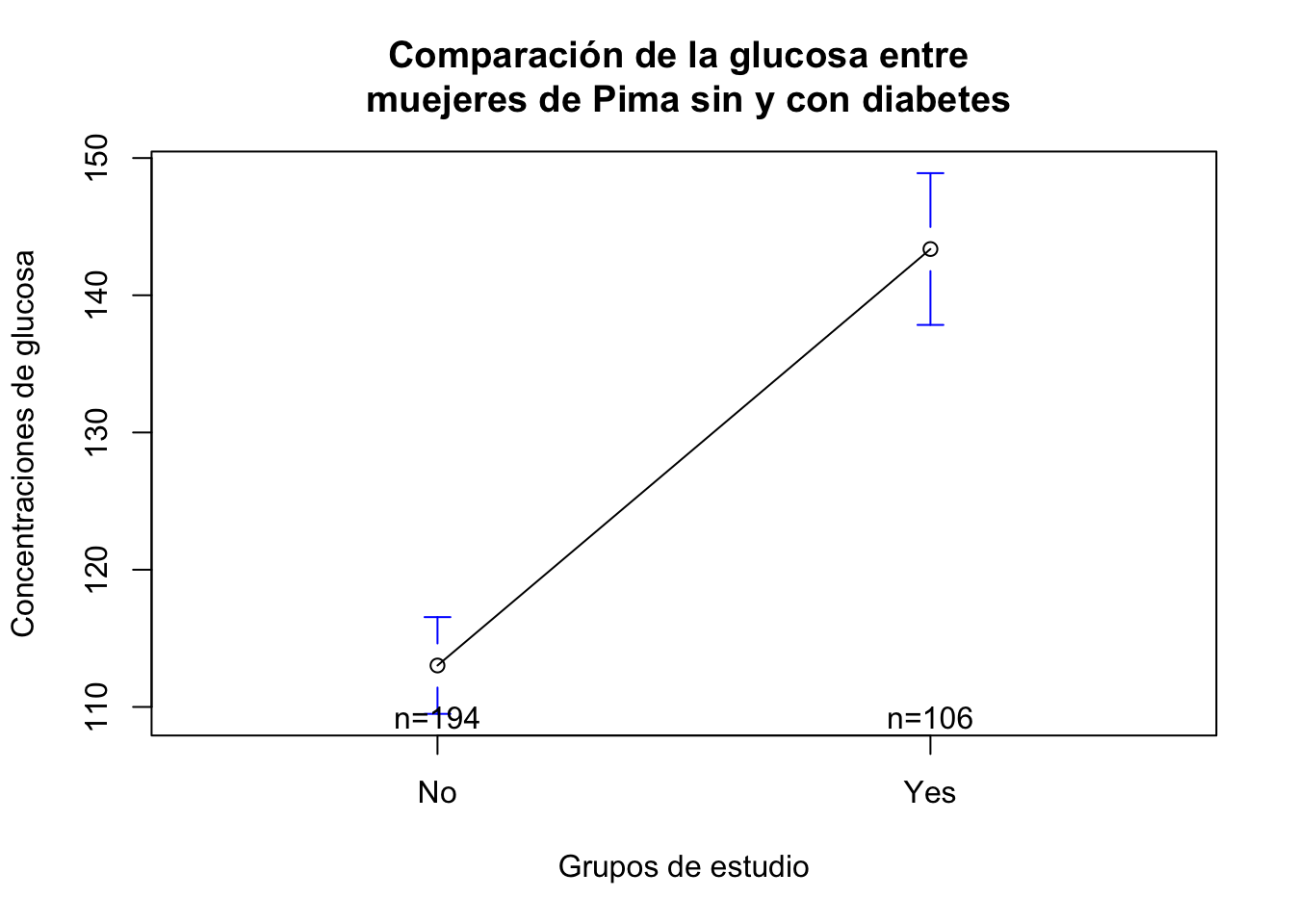
Exercise 15.4 Utilizando la base de datos “Pima.tr” describa si hay diferencias en los niveles de glucosa, la presión arterial, en sikin, índice de masa corporal, en ped y edad entre las mujeres con diabetes y las mujeres sin diabetes. Para este problema utilice únicamente la función t.test de R no realice la prueba de hipótesis por pasos. Para cada una de las variables entregue los siguiente:
- Realice un boxplot para cada variable agrupadando entre las mujeres con diabetes y sin diabetes
- Realice un gráfico de violín para cada variable agrupando entre mujeres con diabetes y sin diabetes
- Realice un gráfico de
plotmeanspara cada variable agrupando entre mujeres con diabetes y sin diabetes - Resultado de la prueba \(t-student\)
- Conclusión
Resolución ejercicio Exercise 15.4
Se muestran solo resultados para glucosa
# Importar base
library(MASS)
Attaching package: 'MASS'The following object is masked from 'package:dplyr':
selectdata("Pima.tr")# Gráficos
## Boxplot
boxplot(Pima.tr2$glu~Pima.tr2$type, # Datos
lwd = 2, # Lines width
col = c("#76EEC6", "#FFE4C4"), # Color
xlab = "Grupos", # X-axis label
ylab = "Concentraciones de glucosa", # Y-axis label
main = "Comparación de la glucosa entre muejeres de Pima sin y con diabetes", # Title
border = "black", # Boxplot border color
outpch = 25, # Outliers symbol
outbg = "green", # Outliers color
whiskcol = "blue", # Whisker color
whisklty = 2, # Whisker line type
names=c("Muejeres sin diabetes", "Muejres con diabetes"), #Nombres de los grupos
lty = 1) # Line type (box and median)
# Gráficos
## Violín
vioplot::vioplot(Pima.tr2$glu~Pima.tr2$type, # Datos
col = c("#76EEC6", "#FFE4C4"), # Color
xlab = "Grupos", # X-axis label
ylab = "Concentraciones de glucosa", # Y-axis label
main = "Comparación de la glucosa entre \n mujeres de Pima sin y con diabetes", # Title
names=c("Muejeres sin diabetes", "Muejres con diabetes"))
# Graficos
## Plot means
gplots::plotmeans(Pima.tr2$glu~Pima.tr2$type, # Datos
ylab = "Concentraciones de glucosa", # Y-axis label
xlab = "Grupos de estudio",
main = "Comparación de la glucosa entre \n muejeres de Pima sin y con diabetes", # Title
)
# Evaluación de la homgenidad de varianzas
car::leveneTest(Pima.tr2$glu~Pima.tr2$type)Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 1 4.2982 0.03901 *
298
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1t.test(Pima.tr2$glu~Pima.tr2$type, var.equal=F)
Welch Two Sample t-test
data: Pima.tr2$glu by Pima.tr2$type
t = -9.162, df = 191.43, p-value < 2.2e-16
alternative hypothesis: true difference in means between group No and group Yes is not equal to 0
95 percent confidence interval:
-36.88061 -23.81400
sample estimates:
mean in group No mean in group Yes
113.0206 143.3679 Exercise 15.5 Utilizando la base de datos “Pima.tr” describa si hay diferencias en los niveles de glucosa, la presión arterial entre las mujeres con más de 40 años y las que mujeres con 40 años o menos.
Exercise 15.6 La base de datos “SLE dataset1” es una base de datos publica que se utilizó una publicación en la que se intentó asociar las concentraciones de adipocinas con la nefritis lúpica y los valores de proteinuria en pacientes con Lupus Eritematoso Sistémico. La base “SLE dataset1” es un libro de Excel con varias hojas:
- DATASET PONE-D-17-14360R1: Contiene todos los datos y mediciones de los pacientes
- VARIABLES INFORMATION: Contiene una descripción breve de las variables de la hoja anterior. Puede encontrar más información en: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0184056
Utilizando la base de datos SLE dataset1.xls que puede descargar en el siguiente link replique los resultados de la tabla 2 del articulo: Serum levels of adiponectin and leptin as biomarkers of proteinuria in lupus nephritis. La tabla deberá de incluir estadística descriptiva y pruebas de hipótesis tanto para variables cualitativas como cuantitivas. Asuma estadística paramétrica
15.5 Prueba t para variables dependientes
Un método que se utiliza con frecuencia para averiguar la eficacia de un tratamiento o procedimiento experimental es aquel que hace uso de observaciones relacionadas que resultan de muestras no independientes.
- Mediciones a través del tiempo
- Dos mediciones en el mismo sujeto
- Diseño cruzados
En estos casos la prueba de hipótesis más adecuada es la prueba t de student para muestras pareadas. Dado que se trabaja con la diferencia de las medias, no es necesario realizar prueba de homogeneidad de varainzas. !Es la misma muestra!
La estimación del estadístico t, se basa en el siguiente formula donde:
\[ t= \frac{\bar{d}- \mu d_0}{s_{\bar{d}}} \]
Donde:
- \(\bar{d}\) es la diferencia de la media muestral
- \(\mu d_0\) es la diferencia de la media poblacional supuesta
- \(s_{\bar{d}}\) es la desviación estándar de las diferencias divida entre la raíz de \(n\), es decir, \(\frac{s_d}{\sqrt{n}}\)
Vamos a resolver un ejemplo
15.6 Ejercicio práctico para la prueba t student para muestras pareadas
Example 15.2 Nancy Stearns Burgess condujo un estudio para determinar la perdida de peso, la composición corporal, la distribución de grasa corporal y la tasa metabólica en reposo en individuos obesos antes y después de 12 semanas de tratamiento con dieta muy baja en calorías (DMBC), y comparar la hidrodensitometría con el análisis de impedancia bioeléctrica. Los 17 individuos (nueve mujeres y ocho hombres) que participaron en el estudio eran pacientes externos de un programa de tratamiento con base hospitalaria para la obesidad. Los pesos de las mujeres antes y después del tratamiento de 12 semanas de DMBC se muestran en dos objetos. Se pretende saber si estos datos ofrecen suficiente evidencia que permita concluir que el tratamiento es eficaz para reducir el peso en mujeres obesas.
Se crean dos objetos para ello:
antes<-c(117.3, 111.4,98.6,104.3,105.4,100.4, 81.7,89.5,78.2)
despues<-c(83.3,85.9,75.8,82.9,82.3,77.7,62.7,69.0,63.9)Tratamos de probar si:
- Lo que se busca es saber si existe la suficiente evidencia para concluir que el programa de dietas es eficaz.
- Si es posible rechazar la hipótesis nula que indica que el cambio en la media de la población \(\mu_d\) es cero o positivo.
Podemos graficar, el siguiente código tiene objetivo mostrar todos los argumentos de la función boxplot, usted puede copiar y pegar o hacer un gráfico más sencillo:
boxplot(antes, despues, # Datos
horizontal = FALSE, # Horizontal or vertical plot
lwd = 2, # Lines width
col = c("#76EEC6", "#FFE4C4"), # Color
xlab = "Grupos", # X-axis label
ylab = "Peso", # Y-axis label
main = "Comparación del peso antes y después de la intervención", # Title
border = "black", # Boxplot border color
outpch = 25, # Outliers symbol
outbg = "green", # Outliers color
whiskcol = "blue", # Whisker color
whisklty = 2, # Whisker line type
names=c("Peso antes", "Peso despues"), #Nombres de los grupos
lty = 1) # Line type (box and median)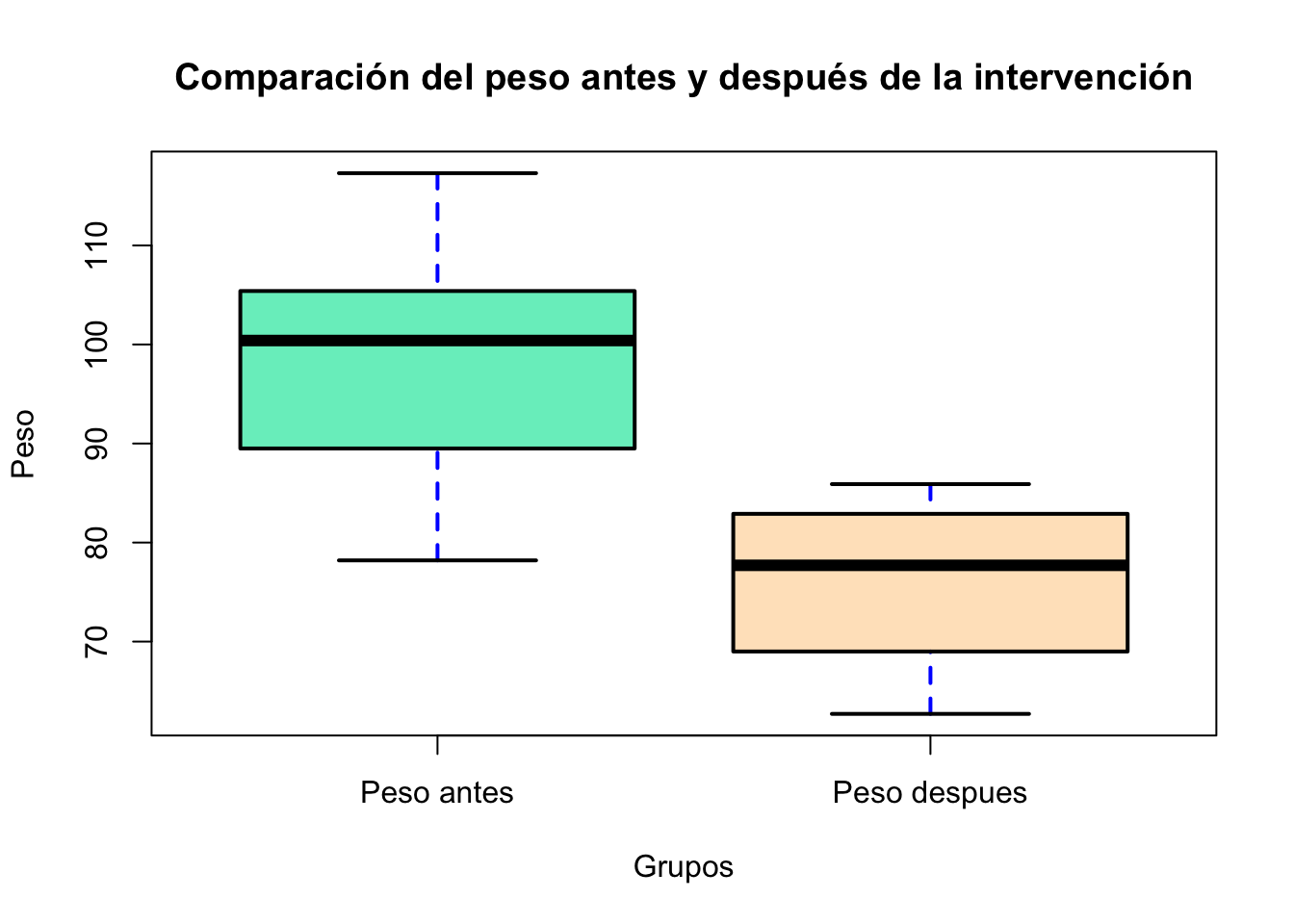
Para realizar la prueba t, puede emplear el siguiente código:
t.test(x=antes, y=despues, alternative = "greater",
paired = T, var.equal = T)
Paired t-test
data: antes and despues
t = 12.74, df = 8, p-value = 6.787e-07
alternative hypothesis: true mean difference is greater than 0
95 percent confidence interval:
19.29166 Inf
sample estimates:
mean difference
22.58889 Note como el grupo 1 es el peso antes y el grupo 2 es el peso después, por lo tanto la hipótesis que buscamos probar es:
\[H_0= \mu_{antes} >= \mu_{después}\] \[H_a= \mu_{antes} < \mu_{después}\] Si la elección de los grupos fuera a la inversa, es decir, si el grupo 1 fuera el peso después y el grupo 2 fuera el peso antes. Las hipótesis deberían plantearse al revés que la descrita anterioremente y el argumento alternative debería ser less
En el caso que nuestra hipótesis sea a dos colas, en R debe de plantearse:
t.test(x=antes, y=despues, alternative = "two.sided",
paired=T, var.equal = T)
Paired t-test
data: antes and despues
t = 12.74, df = 8, p-value = 1.357e-06
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
18.50003 26.67775
sample estimates:
mean difference
22.58889 Note que el único argumento que se debe de cambiar para indicarle a R que la muestra es pareada es: paired=T. Este argumento precisamente, nos permite diferenciar entre una prueba \(t\) para muestras independientes.
15.6.1 Prueba t desde una base datos
Lo primero es organizar los datos del peso antes y peso después en una base de datos:
antes<-c(117.3, 111.4,98.6,104.3,105.4,100.4, 81.7,89.5,78.2)
despues<-c(83.3,85.9,75.8,82.9,82.3,77.7,62.7,69.0,63.9)
# Crear un df para poder utilizar la función como fórmula
Medicion <- rep(x=c("antes", "despues"), each=9, times=1)
Peso <- c(antes, despues)
df <- data.frame(Medicion,Peso)Para realizar la prueba t para muestras pareadas utilizamos el siguiente código:
t.test(df$Peso~df$Medicion, paired=T)
Paired t-test
data: df$Peso by df$Medicion
t = 12.74, df = 8, p-value = 1.357e-06
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
18.50003 26.67775
sample estimates:
mean difference
22.58889 15.6.2 Ejercicios prueba t pareada
Utilizando las base de datos “Base_Prueba_t_pareada” que se encuentra adjunta a esta a tarea o que puede descargar de la carpeta de bases de datos, resuelva los ejercicios utilizando la función t.test. Además, realice gráficos de caja y bigotes y concluya en cada uno de los ejercicios.
La “Base_Prueba_t_pareada” es una base de datos que contiene la mediciones de adipocinas en pacientes con insuficiencia hepática. Contiene mediciones de estas adipocinas séricas a distintos tiempos: Basales, 3 meses, 6 y 12 meses. Puede descargar la base de datos aquí
Exercise 15.7 ¿Existe evidencia para demostrar que los pacientes con insuficiencia hepática presentaron algún cambio entre las mediciones basales de leptina (Leptin) y las mediciones de leptina a los 12 meses (Leptin12M)?
- Realice los gráficos adecuados
- Realice la pruea de hipótesis pertinente para responder la pregunta
Exercise 15.8 Los investigadores asignaron una intervención para reducir las concentraciones de adiponectina en los pacientes con insuficiencia hepática, para ello realizaron mediciones basales de esta adipocina (Adiponectin) y mediciones a los 6 meses (Adiponectin6M) y a los 12 meses (Adiponectin12M). ¿Pueden concluir los investigadores que se presentó una disminución de las concentraciones séricas de adiponectina?
- Realice los gráficos adecuados
- Realice la pruea de hipótesis pertinente para responder la pregunta
Exercise 15.9 Los investigadores a cargo del estudio realizaron la medición de un biomarcador que se asocia a una enfermedad más grave en los pacientes con insuficiencia hepática, se ha validado que a mayores concentraciones de este biomarcador se presenta una enfermedad más grave. ¿Existe evidencia para demostrar que los pacientes empeoraron a los 6 meses y a los 12 meses con respecto a la medición basal?. La variable “Biomarcador” tiene las mediciones basales del biomarcador de interés. Mientras que variables “Biomarcador6M” y “Biomarcador12M” las mediciones a los 6 y 12 meses
- Realice los gráficos adecuados
- Realice la pruea de hipótesis pertinente para responder la pregunta
15.7 Librería ggsataplot
Una de las librerías más potentes para visualizar datos y hacer pruebas de hipótesis es ggstatplot. Esta liberería es es una extensión del paquete ggplot2 para crear gráficos con detalles de pruebas estadísticas incluidas en los propios gráficos ricos en información. Puede consultar un poco más de información aquí
Para instalar la librería utilice el siguiente código:
install.packages("ggstatsplot")El código que utiliza ggstatplot es código que está basado en tydiverse, por lo que pudiera resultarle un poco diferente, al código clásico de R.
Supongamos que es de nuestro interés comparar la edad entre al pacientes con y sin diabetes de Pyma utilizando la base de datos Pima.tr2, el código para realizar esta prueba t de student de muestras independientes sería:
# Importar baese
library(MASS)
data("Pima.tr2")ggstatsplot::ggbetweenstats(
data=Pima.tr2,
x="type", # el nombre de la variable que quiere colocar en el eje de las x, debe ser un factor y utilizar comillas
y= "age", # Nombre de la variable cuantitativa en comillas
type = "parametric" # Para indicar que la prueba que necesitamos es una prueba paramétrica
)Warning in min(x): no non-missing arguments to min; returning InfWarning in max(x): no non-missing arguments to max; returning -Inf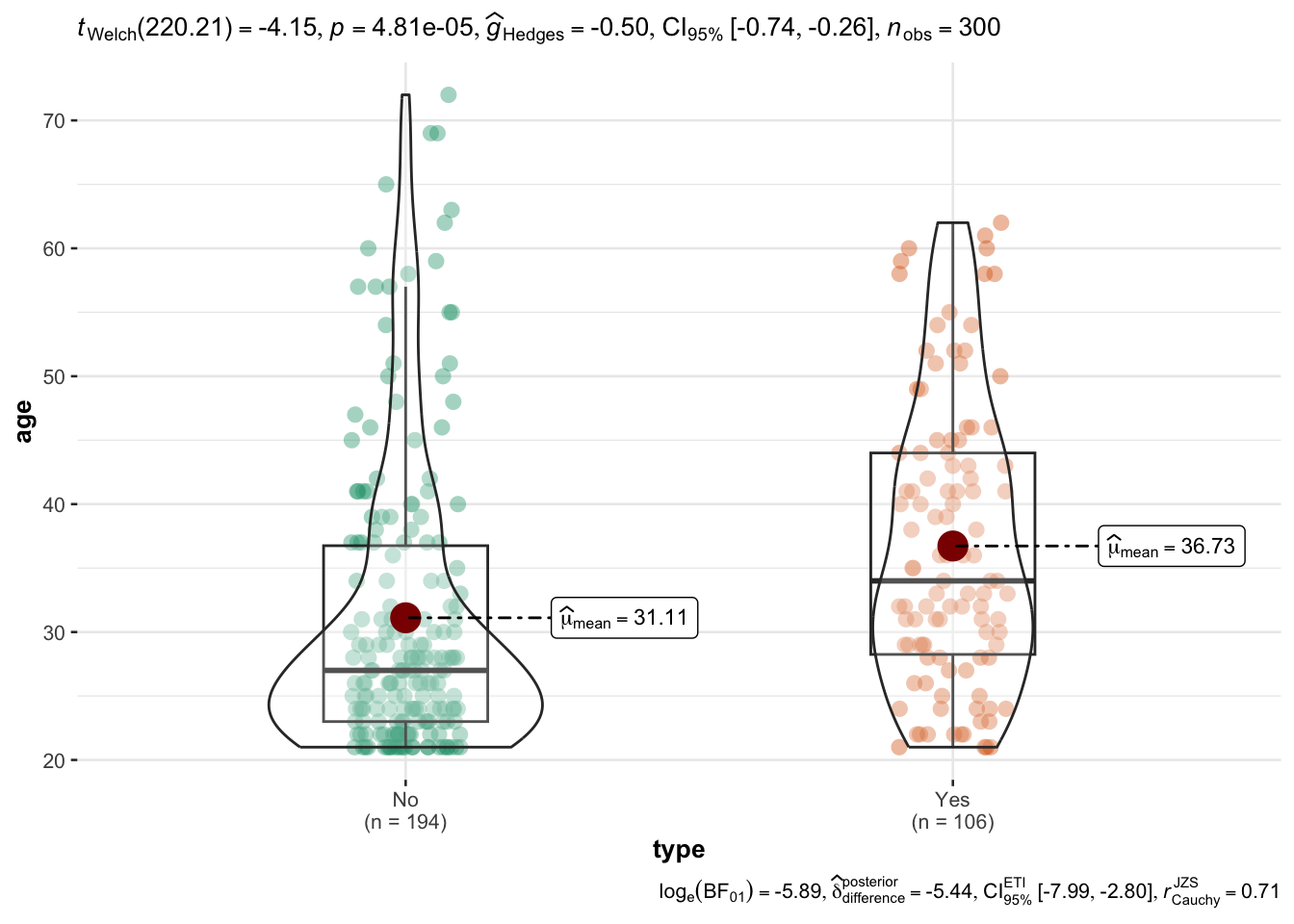
Si el factor tiene más de dos niveles, la función devolverá ANOVA. Note como la información que proporciona incluye: - Valor del estadístico t - Intervalos de confianza - Valor de p - Tamaño del efecto - Estadística bayesiana
Si fuera de nuestro interés realizar una prueba pareada, por ejemplo el peso antes y el peso después, el código sería:
ggstatsplot::ggwithinstats(
data = df,
x = Medicion,
y = Peso,
title = "Comparación del peso antes y después"
)Warning in min(x): no non-missing arguments to min; returning InfWarning in max(x): no non-missing arguments to max; returning -Inf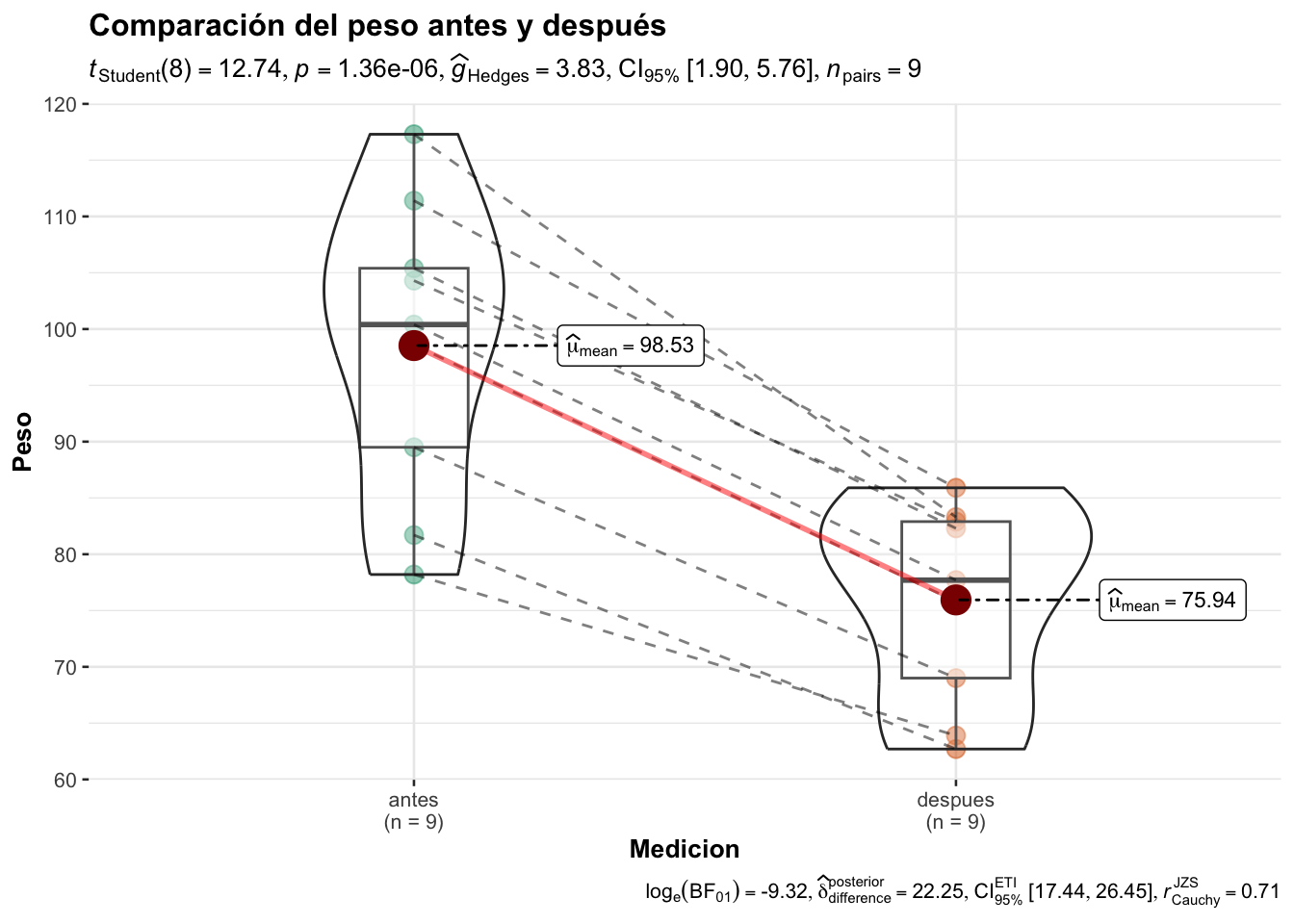
Exercise 15.10 Resuelva los ejercicios del Exercise 15.4 al Exercise 15.9 utilizando la librería ggstatsplot