3 Introducción a la estadística
- Autor: Edsaúl Emilio Pérez Guerrero
- Afiliación: Universidad de Guadalajara
- mail: edsaul.perezg@academicos.udg.mx
- Última actualización: 2024-04-24
En este capitulo se abordarán conceptos básicos de la estadística, se plantearán las diferencias entre estadística y bioestadística y se describirán las etapas del análisis estadístico.
3.1 Conceptos básicos
Es importante que el lector se familiarizarse con algunos conceptos básicos de estadística. “Todos debemos de hablar el mismo idioma”.
3.1.1 Estadística
Consiste en la recolección, cuantificación, síntesis, análisis e interpretación de la información relevante contenida en datos. Existen diversas ramas dentro de ella, como estadística matemática, estadística aplicada, estadística descriptiva y estadística inferencial (Hui 2019), (Alfredo Celis de la Rosa 2014), (Dalgaard 2008).
El objetivo principal de la estadística es obtener información a partir de datos y con ella poder tomar decisiones. La estadística es un campo interdisciplinario; la estadística encuentra aplicabilidad en prácticamente todos las disciplinas (Hui 2019).
3.1.2 Bioestadística
Es la rama de la estadística que se ocupa de los problemas dentro de la ciencias de la vida, como la biología o la medicina entre otras (Martı́nez González; Almudena Sánchez-Villegas; Estefanı́a Toledo Atucha; Javier Faulı́n Fajardo 2020).
Es la aplicación de la recolección, resumen y obtención de conclusiones acerca de las características de los datos enfocada disciplinas de la salud.
Aunque el título de este compendio es Estadística con R para ciencias de la Salud, en realidad se refiere a bioestadística. Es decir este compendio es sobre bioestadística.
3.1.3 Estadística descriptiva e inferencial
Dentro existen dos ramas que se encuentra profundamente ligadas una con la otra. Incluso, para fines práctico se pueden considerar como dos etapas. La primera de ellas, es la Estadística descriptiva la cual tiene objetivo presentar y organizar los datos; es decir, la estadística descriptiva nos permite simplificar y comprender una gran cantidad de datos mediante la generación de tablas, gráficas y la obtención de algunos parámetros que describen a estos datos (Martı́nez González; Almudena Sánchez-Villegas; Estefanı́a Toledo Atucha; Javier Faulı́n Fajardo 2020), (Alfredo Celis de la Rosa 2014).
Por otro lado, la Estadística inferencial nos permite tomar decisiones a partir de una cierta cantidad de datos (muestra) y trasladarlo a una población (totalidad de los datos). Se podría decir, que el primer paso es presentar, organizar y entender los datos (estadística descriptiva) y después tomar decisiones (hacer inferencias) utilizando la estadística inferencial (Martı́nez González; Almudena Sánchez-Villegas; Estefanı́a Toledo Atucha; Javier Faulı́n Fajardo 2020), (Alfredo Celis de la Rosa 2014).
3.2 Universo, población y muestra
Universo En ciertas ocasiones nos enfocamos en pacientes que tienen ciertas características y nos referimos a ellos como universo o población. En este sentido, en estadística universo o población se definen como el conjunto de valores por los cuales existe algún interés. Por ejemplo, nuestro universo o población de trabajo puede ser los pacientes con diagnóstico de artritis reumatoíde de un hospital de un segundo nivel de entre 18 y 45 años. Todos ellos serán nuestro universo o población. Las características de nuestra población pueden ser diversas y muy variadas por ejemplo, límites geográficos, grupos de edad, límite de tiempo, sexo etc.(Alfredo Celis de la Rosa 2014)
La población se representa con la letra mayúscula \(N\).
Muestra. En la mayoría de las ocasiones, no nos es posible trabajar con el total de la población o universo. Ya sea por factibilidad o por que es imposible identificar la totalidad de la población. La muestra debe cumplir con ciertas características como ser representativa, homogénea, independiente, de suficiente tamaño y aleatoria. En los próximos capítulos profundizaremos un poco más en como seleccionar esta muestra.
3.3 Parámetros y estadísticos
Los datos que podemos obtener de una muestra y una población son distintos. Por ejemplo, supongamos que nuestra población de interés son todos los alumnos de posgrado del Centro Universitario de la Salud. Si calculamos la media de la edad de estos alumnos, estaremos resumiendo los valores y obteniendo atributos de la población. Esto es un parámetro. En cambio, si este calculo lo hacemos para una muestra de la población de alumnos de posgrado, estaremos calculado un estadístico o estimador. El estadístico será solamente una aproximación de un parámetro. En cuanto más representativa sea la muestra el estadístico más se aproximará al parámetro (Dalgaard 2008), (Martı́nez González; Almudena Sánchez-Villegas; Estefanı́a Toledo Atucha; Javier Faulı́n Fajardo 2020).
Las diferencias entre parámetro y estadístico las podemos resumir de la siguiente forma:
- Una estadístico es una característica de una pequeña parte de la población, es decir, una muestra. El parámetro es una medida fija que describe la población objetivo.
- El estadístico es variable, depende de la muestra de la población en cambio el parámetro es un valor numérico fijo y desconocido.
- Las notaciones para parámetro y estadístico son diferentes. Los parámetros son representados utilizando letras griegas, por ejemplo, la letra \(\mu\) para la media, \(\sigma\) para la desviación estándar etc. Por su parte, los estadísticos se representan de forma distinta. \(\bar{x}\) representa la media como estadístico, la letra \(s\) representa la desviación estándar muestra etc.
3.4 Tipos de variables
La materia prima de la estadística son los datos, precisamente el principal objetivo de la estadística es procesar los datos para obtener información. En este compendio vamos a trabajar con datos, los vamos a procesar, entender, presentar y con ellos vamos llegar a conclusiones.
Los datos, normalmente contienen ciertas características que conforman nuestra población.Las variables son la que contienen estás características y pueden ser de diferentes tipos. Por ejemplo, en el data frame bacteria del capitulo @ref(R-lab-01) se presentaron variables como edad, tiempo de duración de la infección, grupo de estudio, entre otros. Estás variables representan las características de los 220 pacientes pediátricos incluidos en el estudio. En el data frame bacteria hay variables que se refieren a números, como la edad y el tiempo de duración de la enfermedad. Pero hay otros que ofrecen una cualidad de lo pacientes, por ejemplo si esté presentó otitis o no. Por tanto, las variable se pueden clasificar. De esta clasificación dependerá la forma en la que procesemos y analizemos.
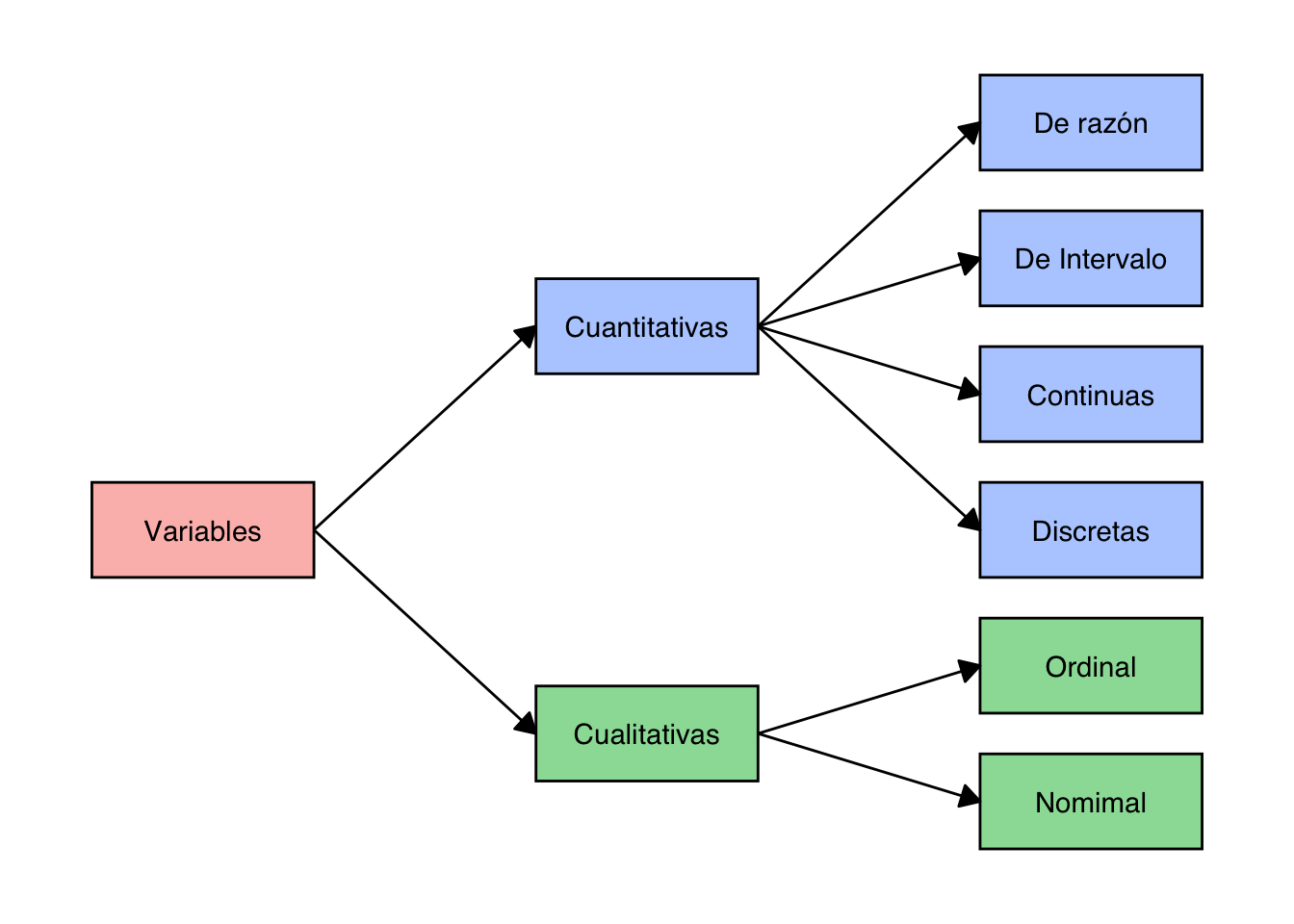
La manera más amplia en la que podemos clasificar a las variables es cualitativa y cuantitativa. Una variable cualitativa representa una cualidad o característica del individuo, por ejemplo la variable que indica si el paciente solamente recibió placebo o alguno de los tratamientos. En cambio, una variable cuantitativa, es un poco más fácil de definir. Las variables cuantitativas son aquellas que se expresan como valores numéricos. Sin embargo, la clasificación es más amplia que lo descrito anteriormente. La figura @ref(fig:fig9) muestra una visión general de los tipos de variables.
La siguiente lista muestra los principales tipos de variables, al final de cada descripción se indica si esta es cualitativa o cuantitativa.
Binaria: este es el tipo de variable más simple, con solo dos respuestas posibles. Por ejemplo, fumador y no fumador; paciente y control. Cualitativa
Nominal: este tipo de datos de cadena de caracteres es una versión más general de una variable binaria y tiene un número fijo de respuestas posibles que no pueden ordenarse de manera útil. Suelen estar codificadas alfanuméricamente establecidas por el investigador. Por ejemplo: Casado, soltero, divorciado, viudo. Cualitativa
Ordinal: las posibles respuestas para este tipo de datos de cadena de caracteres están ordenadas linealmente. Podemos saber que un dato es mayor que otro, pero no podemos decir exactamente cuanto. Estás variables se pueden ordenar. Por ejemplo: Normopeso, sobrepeso y obesidad. Sabemos que el paciente con obesidad pesa más que el paciente con sobre peso y este a su vez más que el paciente con normopeso. A pesar de que existen rangos para definir esta variable, no podemos decir con exactitud cuanto más o cuanto menos es una de las categorías. Cualitativa
Discreta: variables numéricas que no pueden dividirse. Por ejemplo la edad medida en años o el número de pacientes. Cuantitativa.
Continuas: datos numéricos cuyo número entero está seguido por decimales. Por ejemplo el peso medido en kg. Cuantitativa
Las variables cuantitativas también pueden clasificar según tengan o no en su escala un valor de cero absoluto
Intervalo: No incluye el cero absoluto. Por ejemplo la medición de la temperatura en grados celsius. Cuantitativa
De razón: Incluyen el cero absoluto. Por ejemplo la medición de la temperatura en grados kelvin. Cuantitativa
Indexación:* por lo general, son nombres, etiquetas, números de caso o números de serie que identifican a un encuestado o grupo de encuestados. Este variable aunque que podría clasificarse como cualitativa, solamente se utiliza para identificar los datos en un data frame.
Para R el tipo de variables es un tanto distinta al de la lista, pero este tema lo abordaremos en el capitulo @ref(R-lab-02).
3.5 Ejercicios capitulo 3
Los siguientes ejercicios tienen como objetivo reforzar la identificación de variables.
Exercise 3.1 Utilizando la siguiente lista de variables realice una clasificación de las mismas en cualitativa y cuantitativa. Indicando además, a que tipo de variable corresponde dentro de esta clasificación: variables cualitativas (nominal, dicotómica u ordinal) y cuantitativas (discretas, continuas, de intervalo o de razón)
Edad de un grupo de infantes expresada en meses
Índice tabáquico. Es una variable que indica el riesgo de padecer complicaciones derivadas de fumar como se muestra a continuación:
Índice Clasificación < 10 Sin riesgo 10-20 Riesgo moderado 21-41 Riesgo intenso 41> Alto riesgo - Escala del dolor medida como: mucho, poco o nada
Estado civil de los pacientes
Presencia o ausencia de comorbilidades
Índice de masa corporal
Medición de la actividad de la enfermedad con un índice que tiene puntajes que van desde 0 hasta 105. Solamente se pueden tener números enteros
Número de embarazos
Glucosa en ayunas expresada en mg/dL
Las reacciones adversas a los medicamentos se clasifican en reacciones de Tipo A, Tipo B, Tipo C, Tipo D, Tipo E y Tipo F. Una definición operativa de estás se muestra enseguida:
- Tipo A: Las reacciones adversas tipo A, son aquellas que se observan con más frecuencia, se caracterizan por que son dependientes de la dosis administrada, reduciendo la dosis se consigue la desaparición del efecto
Tipo B: Son menos frecuentes que las anteriores, la principal característica que las diferencia es que no son dosis – dependientes. Son debidas a mecanismos inmunológicos (reacciones alérgicas) y farmacogenéticos. Este tipo de reacciones presentan una mortalidad elevada y el tratamiento consiste en suspender la administración.
Tipo C: Aparecen tras la administración prolongada de un fármaco, en general son previsibles y conocidas, se incluyen en este grupo la farmacodependencia, la discinesia tardía por neurolépticos o el síndrome de Cushing por corticoides.
Tipo D: Son poco frecuentes, aparecen un tiempo después de suprimir la administración del fármaco, se incluyen la teratogénesis y la carcinogénesis.
Tipo E: Aparecen tras la supresión muy brusca de un fármaco, por ejemplo, la insuficiencia suprerenal tras la supresión de corticoides, las crisis comiciales tras la supresión de antiepilépticos o la angina tras la supresión de beta – bloqueante
Tipo F: No son debidas al fármaco sino a impurezas, excipientes o contaminantes. También se incluyen en este grupo las causas por medicamentos caducados.
Exercise 3.2 El siguiente ejercicio muestra la descripción de la base de datos birwht. De acuerdo con esta descripción clasifique a cada una de las variables de la lista.
La base de datos birthwt tiene 189 filas y 10 columnas. Los datos se recopilaron en el Baystate Medical Center, Springfield, Mass durante 1986. Las variables:
low: indicator of birth weight less than 2.5 kg.
age: mothers age expressed years.
lwt: mothers weight expressed pounds at last menstrual period.
race: mothers race (1 = white, 2 = black, 3 = other).
smoke: smoking status during pregnancy.
ptl: number of previous premature labours.
ht: history of hypertension.
ui: presence of uterine irritability.
ftv: number of physician visits during the first trimester.
bwt: birth weight expressed grams.
Exercise 3.3 El siguiente ejercicio muestra una descripción de la base de datos Pima.tr. Clasifique las variables de la lista. La base de datos Pima.tr contiene los datos de una población de mujeres que tenían al menos 21 años de edad, descendientes de indígenas pima y que vivían cerca de Phoenix, Arizona, se sometieron a pruebas de diabetes de acuerdo con los criterios de la Organización Mundial de la Salud. Los datos fueron recopilados por el Instituto Nacional de Diabetes y Enfermedades Digestivas y Renales de EE. UU. Utilizamos los 532 registros completos después de descartar los datos (principalmente faltantes) sobre la insulina sérica. Las variables de este data frame son:
npreg: number of pregnancies.
glu: plasma glucose concentration at an oral glucose tolerance test.
bp: diastolic blood pressure (mm Hg).
skin: triceps skin fold thickness (mm).
bmi: body mass index (kg/(m)2.
ped: diabetes pedigree function.
age: age expressed years.
type: Yes or No, diagnostic diabetic according to WHO criteria.