set.seed(4)# Función para que todos tengamos los mismos datos
sample(x=1:2000, size=10, replace = FALSE) [1] 1528 587 819 1795 71 684 371 757 698 307En este capítulo abordaremos los conceptos de población y muestra y muestreo. Revisaremos las ventajas y desventajas de cada uno de los tipos de muestreo y algunos ejercicios en R.
En estadística una población puede entenderse como el grupo objetivo del cual se eligen los sujetos de la muestra y para quienes se generalizarían los resultados. Elgrupo objetivo debe tener características previamente definidas. Algunos ejemplos de población son:
Refiriéndonos a la definición de población, podemos decir que está formada por todas las unidades sobre las que se pueden aplicar los resultados de la investigación. En otras palabras, la población es un conjunto de todas las unidades que poseen características variables bajo estudio y para las cuales los resultados de la investigación pueden generalizarse (Abhaya Indrayan 2017), (Majid 2018), (Shukla 2020).
El concepto de población no es perfecto y presenta algunas limitantes, por ejemplo:
En algunas ocasiones nos podemos referir a una población finita o población infita. El primer concepto se refiere a una población en el que las unidades se encuentran perfectamente definidas y podemos estimar cuantas unidades conforman las misma. Por ejemplo: todas las mujeres casadas mayores de 40 años del barrio del Santuario en Guadalajara Jalisco. En cambio, una población infita, no puede ser contabilizada. Por ejemplo: la cantidad de diabéticos de México. Aunque existen estimaciones de cuantos diabéticos hay en México, es imposible saber con exactitud cuantos hay.
En la sección de [Universo, población y muestra] ya se definió el concepto de muestra. Aquí nos enfocaremos en sus ventajas y desventajas. Algunas de las características de la muestra son:
Puede ser el único método factible para la recopilación de datos relevantes en algunos casos. Ventaja
Menor costo y menor demanda de recursos (personal, laboratorio, etc.) Ventaja
Se puede recopilar información confiable si lo métodos son adecuados. Ventaja
Una muestra de una población con toda probabilidad será diferente de la segunda muestra. Desventaja
No todas las muestras son representativas, aunque hay métodos disponibles que hacen que sea probable que suceda. Desventaja
Cuando se requiere información para segmentos pequeños que contienen pocos individuos, el muestreo puede no proporcionar información lo suficientemente precisa sobre ellos. Desventaja
A veces, de todos modos, se necesita un recuento completo, como para un diagnóstico y perfil de resultados de los casos ingresados en un hospital cada año. Desventaja
Para comprender con exactitud los conceptos de muestreo, es necesario antes definir otros conceptos “para hablar el mismo lenguaje”
La unidad de investigación es el tema sobre el que se obtiene información. En cambio, la unidad de muestreo es la que se utiliza para realizar el muestreo. Para poder comprender mejor estos conceptos, revisaremos un ejemplo: En un censo realizado por el INEGI (Instituto Nacional de Estadística y Geografía) sobre la desnutrición infantil, la unidad de muestreo podría ser una familia, pero la unidad de investigación podría ser un niño menor de 5 años. Una unidad de muestreo puede tener múltiples unidades o ninguna unidad sobre la cual investigar.
Se refiere a la lista de todas las unidades de muestreo en la población objetivo se denomina marco de muestreo. Algunas características del marco de muestreo son:
¿Qué cantidad de muestra es la adecuada para ser representativa de una población? La respuesta a esta pregunta es el tamaño de muestra. Este concepto se refiere al número de sujetos o unidades de muestreo mínimos para identificar diferencias. Debe ser lo suficientemente grande para responder nuestra pregunta de investigación y para permitirnos encontrar diferencias y/o asociaciones. Se utiliza la letra \(n\) para referirnos a ella.
En futuros capítulos abordaremos un poco más acerca del tamaño de muestra.
Una muestra se denomina aleatoria cuando la inclusión o exclusión de un sujeto elegible en particular depende del azar y no se puede predecir de antemano (Palinkas et al. 2015),(Berndt 2020).
La selección aleatoria es solo una estrategia para obtener una muestra representativa. Cuanto mayor sea la muestra en relación con el tamaño de la población, mayor será la probabilidad de que sea representativa, aleatoria o no. Pero el muestreo aleatorio asigna probabilidades que ayudan a hacer inferencias estadísticamente sólidas.
Algo que no debemos olvidar es que la fluctuación de la muestra depende del: + Método del muestreo + Tamaño de muestra + Variación
En esta sección se revisaran los siguientes métodos de muestreo(Berndt 2020),(Abhaya Indrayan 2017)
Algunos de los tipos de muestreo no serán definidos en primera instancia pero si serán puestos es práctica.
En el muestreo aleatorio simple todos los individuos o unidades de muestreo deben de tener la misma probabilidad de ser seleccionados. En este tipo de muestreo estrictamente, todas las muestras, independientemente de su tamaño, tienen las mismas posibilidades de ser seleccionadas. Una de las principales desventajas de este tipo de muestreo es que requiere de la disponibilidad del marco muestral.
Por ejemplo, suponga que quiere hacer un muestreo aleatorio en el que su población de interés son los estudiantes de posgrado de CUCS, para ello necesitará una lista de todos los estudiantes que cumplan con sus criterios (incluidos maestrías, doctorados y especialidades). Es decir, se necesita todo su marco de muestreo para seleccionar aletoriamente a los estudiantes.
Según la RAE un estrado es un conjunto de elementos que, con determinados caracteres comunes, se ha integrado con otros conjuntos previos. Ahora imagine, que se realiza un estudio para evaluar los niveles de una hormona en mujeres. Se espera que la muestra sea representativa de todos los hospitales de segundo nivel de Guadalajara. ¿Cómo nos aseguramos de que todos los hospitales tengan una representación adecuada? Para ello, recurrimos al muestro estratificado, para ello se siguen los siguientes pasos:
En el muestreo por estratos, la población se divide en subgrupos o estratos homogéneos basados en una característica específica, como la edad, el género, la ubicación geográfica, el nivel socioeconómico o la condición de salud. Luego, se selecciona una muestra aleatoria de cada estrato. Para el ejemplo anterior podrían los estratos podrían ser: mujeres menores a 20 años, mujeres de entre 20 y 40 años y mujeres mayores a 40 años. La figura Figure 5.1 ilustra el muestreo por estratos:
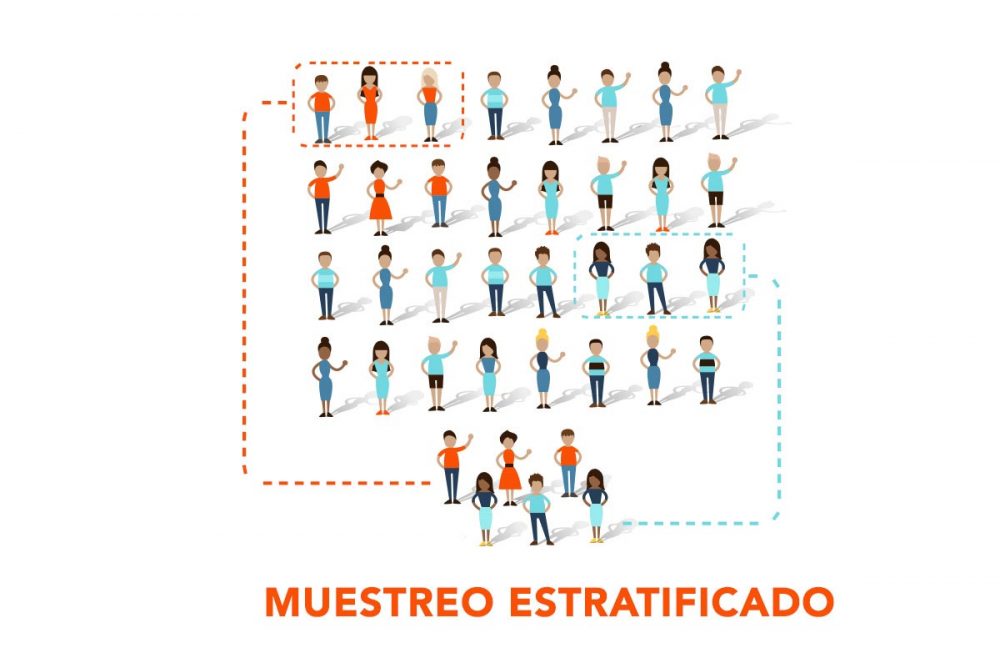
Otro ejemplo de muestreo por estratos es:
Alguna de las ventajas para el muestreo por estratos son:
Mientras que algunas de sus desventajas son:
El muestro aleatorio por clústers suele confundirse con el muestreo por estratos, sin embargo, a diferencia del análisis por estratos, el análisis por clusters permite que ciertas unidades de muestreo, sobre todo cuando son pequeñas o reúnen ciertas características, no sean incluidas. Es decir, podemos no incluir algunas unidades de muestreo con tamaño pequeño. Otra diferencia es que el muestro por conglomerados es una técnica que aprovecha la existencia de grupos que pueden estar definidos previamente (por ejmplo, geográficamente). Por lo tanto, en el muestro de clusters es mejor para divisiones. Puede ver algunos ejemplos sobre el muestro por clusters y sus diferencias entre el muestro por estratos en las figuras Figure 5.2 y Figure 5.3.
Quizá la diferencia más importante entre el muestreo por clústers y por estratos es que el primero se aprovecha de divisiones ya hechas en la población.
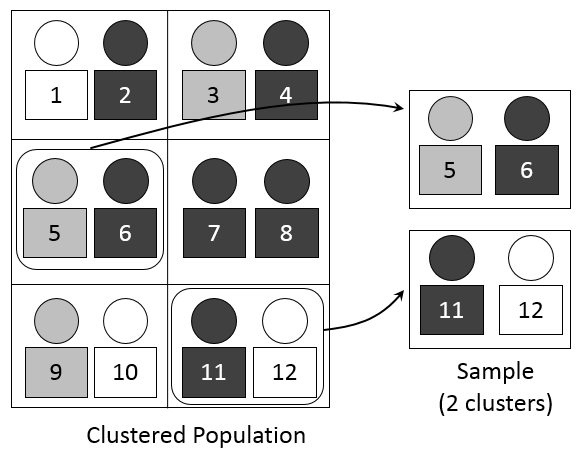

Un ejmploe de muestreo por conglomerados podría ser: imagine que realiza un estudio para evaluar la prevalencia de enfermedades transmitidas por vectores, como el dengue y el zika, en una región rural de un país. En lugar de realizar un muestreo por estratos, donde dividirías la población en grupos basados en alguna característica específica, optas por el muestreo por clusters debido a la falta de una lista completa y actualizada de todos los hogares en la región
Otro tipo de muestreo muy utilizado es el muestro aleatorio multietapa. El cual, como su no nombre lo dice consiste en extrear una muestra por etapas. Por ejemplo, imaginemos que es de nuestro interés estimar la prevalencia de tabaquismo en el estado de Jalisco. Para ello, se puede, por ejemplo, seleccionar primero 4 municipios del estado, luego 12 ciudades dentro de cada municipio seleccionado y luego 50 familias dentro de cada bloque seleccionado, todo por método aleatorio.
El muestreo multietapa es útil para poblaciones de gran tamaño que consiste en extraer las muestras por etapas y Se realiza el muestreo de la unidad mayor a unidad menor.

Imaginemos ahora que tenemos un grupo de niños de una escuela primaria en el que los niños que se encuentran ordenados por estatura. Nuestro interés es conocer el índice masa corporal promedio de los niños de esa primaria. Para poder tener una muestra representativa de estos, se realizará una muestreo aleatorio sistemático. Este tipo de muestro consiste en seleccionar uno de los niños a azar (por ejemplo, mediante un muestreo aleatorio), posteriormente “sistemáticamente” selecciona el siguiente niño. Por ejemplo, podemos seleccionar un niño y medir su índice de masa corporal cada 20 niños. Es decir, después de 20 niños un niño será seleccionado. Con esto, nos aseguramos que por ejemplo no estemos haciendo nuestro muestreo con sesgo. Es decir, tendrías un error si solo seleccionamos a los niños más pequeños o a los más grandes. Ver figura Figure 5.5
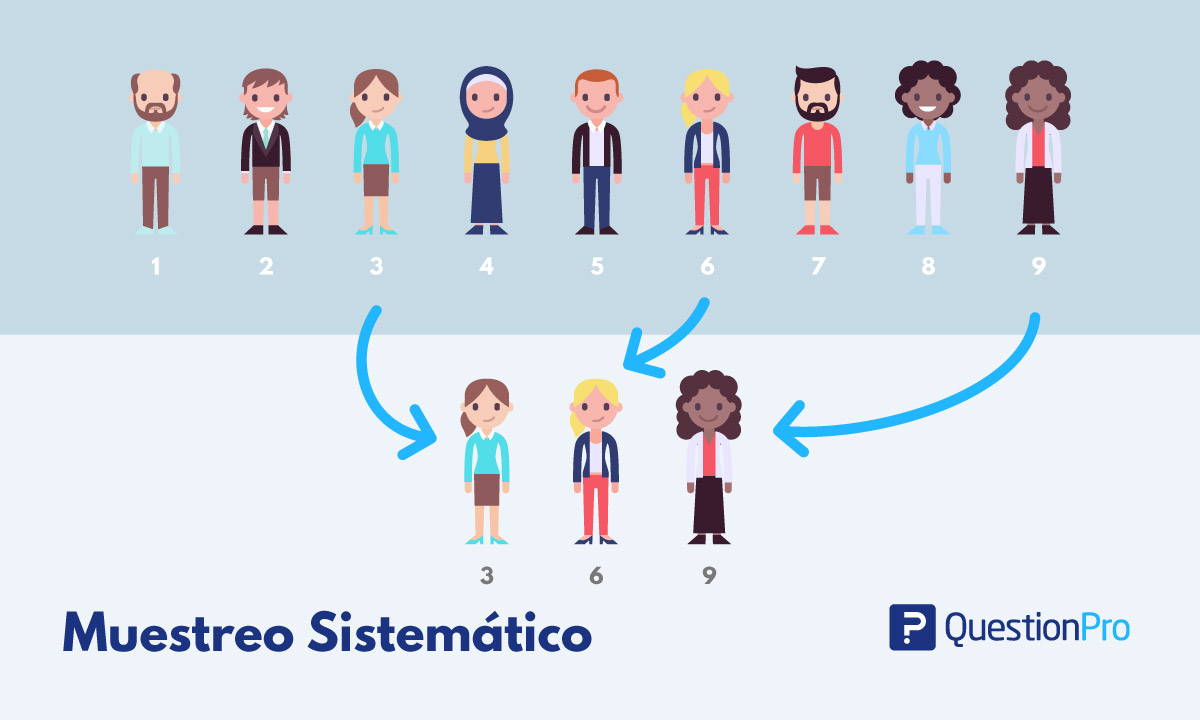
Consiste en incluir a un individuo o paciente siempre y cuando cumplan los criterio de inclusión en el momento que este acuda a consulta, centro de referencia, laboratorio etc. Es un tipo de muestreo no probabilístico, los individuos no tienen las mismas probabilidades de ser seleccionados. Si el paciente no va a consulta no podrá ser seleccionado. En este tipo de muestreo se debe de evitar el sesgo del os días. Por ejemplo, si acudimos a la consulta solamente los lunes, no podríamos seleccionar a los pacientes que acuden otros días.
En el muestreo secuencial, los sujetos elegibles de la población objetivo se seleccionan uno a uno de manera aleatoria y se evalúan. El muestreo posterior se detiene tan pronto como se dispone de un resultado fiable en un sentido u otro. Por ejemplo, si es de nuestro interés asociar el índice de masa corporal con el riesgo de presentar infarto agudo al miocardio, detendremos el muestreo cuando logremos ver esta asociación. Este método de muestreo no es tan popular en medicina y se trata de un método no probabilístico.
REl siguiente apartado de este capítulo describe algunas funciones útiles para realizar muestreo dentro de R. Veremos los siguientes puntos:
sampledyplrRLa función sample() devuelve un número determinado de datos de un objeto. Esta función requiere al menos los siguientes argumentos: + un objeto del que vamos a extraer los datos + la cantidad de datos que vamos extraer + un argumento lógico para indicar si se quiere remplazo
Un argumento es el parámetro(s) proporcionados a una función para realizar las operaciones para las que fue creada. Es decir, un argumento le dice a una función que hacer. En este compendio utilizaremos constantemente la expresión “la función se alimenta de los siguientes argumentos”.
Ejemplo Example 5.1
Example 5.1 De una lista de 2000 datos vamos a extraer 10 de ellos sin remplazo
set.seed(4)# Función para que todos tengamos los mismos datos
sample(x=1:2000, size=10, replace = FALSE) [1] 1528 587 819 1795 71 684 371 757 698 307El ejemplo Example 5.1 requiere de la explicación de algunos puntos:
set.seed permite generar números “aleatorios” bajo ciertos parámetros. En R los números aleatorios, en realidad no son aleatorios, sino pseudoaleatorios. Imagina que tiene un puñado de semillas, y no conoce su procedencia ni el árbol al que darán vida. Por lo tanto, se las siembra, el árbol que crecerá será un misterio. Ser pseudoaleatorio en lugar de aleatorio puro significa que, R necesita conocer la la procedencia de la semilla antes de plantar un árbol. La función set.seed permite modificar esta semilla e indicarle a R cual semilla seleccionar en lugar de seleccionar una al azar.sample generamos de nuestro argumento x 10 números aleatorios (size) sin remplazo. Explicado de otro forma, del argumento x que contiene una secuencia de números del 1 a 2000 se seleccionaron al azar 10 número sin remplazo. El argumento replace indica si la muestra será seleccionada sin o con reemplazo.Exercise 5.1 Cree un objeto con todos los nombres de los los alumnos de la clase. Extraiga una muestra aleatoria con reemplazo de 50.
Exercise 5.2 Función sample() aplicada a bases de datos
De la base de datos pima.tr2 de la librería mass utilizando la variable edad, seleccione al azar 20 datos
El Example 5.2 muestra como realizar muestreo sistemático utilizando R.
Example 5.2
set.seed(4) # Indicamos la semilla a sembrar
n <- sample(Pima.tr2$ID, size=20)# Seleccionar una muestra de 20 sin reemplazo
n+5 # Seleccionamos sitemáticamente [1] 80 264 76 177 250 191 67 107 135 157 89 260 240 53 181 202 155 59 208
[20] 85El Example 5.3 describe como hacer muestreo aleatorio utilizando la librería dplyr
Example 5.3
# Instalar el paquete dplyr
install.packages("dplyr")
# Otra alternativa de instalación
install.packages("devtools")
devtools::install_github("tidyverse/dplyr")
# Una vez instalada la librería podemos cagarla
library(dplyr) # Librería necesario
# Objeto con una muestra de 20 sin reemplazo:
muestra <- Pima.tr2 %>%
sample_n(size=20, replace=F)
head(muestra) # Visualizar los primeros 6 datos de nuestro objeto npreg glu bp skin bmi ped age type ID
1 2 157 74 35 39.4 0.134 30 No 180
2 6 109 60 27 25.0 0.206 27 No 65
3 9 152 78 34 34.2 0.893 33 Yes 152
4 4 134 72 NA 23.8 0.277 60 Yes 246
5 0 167 NA NA 32.3 0.839 30 Yes 288
6 2 112 86 42 38.4 0.246 28 No 126El Example 5.4 muestra como realizar un muestreo por proporción de casos
Example 5.4
muestra2 <- Pima.tr2 %>%
sample_frac(0.10)# Extraer el 10% de lo casos
head(muestra2) npreg glu bp skin bmi ped age type ID
1 8 133 72 NA 32.9 0.270 39 Yes 278
2 7 103 66 32 39.1 0.344 31 Yes 113
3 0 119 64 18 34.9 0.725 23 No 191
4 2 109 92 NA 42.7 0.845 54 No 228
5 4 123 62 NA 32.0 0.226 35 Yes 258
6 0 125 96 NA 22.5 0.262 21 No 291Exercise 5.3 Suponga que queremos aleatorizar a los participantes en dos grupos (A y B), y queremos aleatorizar una muestra de 50 pacientes.
Exercise 5.4 ¿Por qué la muestra de pacientes no incluyó 25 pacientes en el grupo A y 25 pacientes en el grupo B? ¿Considera que es un muestreo aleatorio?
Exercise 5.5 De la muestra anterior extraiga una segunda muestra que contenga un 60% del total de los casos de la muestra anterior.
Exercise 5.6 Si su interés es tener una muestra con al menos 50 individuos en cada uno de los grupos.¿Qué estrategias podría seguir?¿Su estrategia genera una muestra aleatoria?
Exercise 5.7 Un grupo de investigadores realiza una aleatorización de 30 pacientes con el objetivo de tener 15 individuos en el grupo A y 15 individuos en el grupo B. ¿Se puede considerar esta como una muestra aleatoria?
Exercise 5.8 Utilizando la base de datos Pima.tr2 obtenga una muestra de pacientes con diabetes de 20.